Learning vs Inference

In machine learning, the terms "learning" and "inference" are used often and it's not always clear what is meant. For example, is "variational inference" and neural network "inferencing" the same thing? Usually not!

When the deep learning crowd says "inference", what they mean is "perform a prediction." When the bayesian crowd says "inference", what they really mean is "compute the posterior distribution of a latent variable model"; e.g., for a model p(x, z) = p(x | z)p(z) and data x, compute p(z | x).

When someone says learning, they mean their model has a set of parameters and they need to find a good setting of those parameters; e.g. their model is actually p(x, z) = p(x | z; theta)p(z) and they want to find theta. For frequentists, this means finding a point estimate of the parameters. For a bayesian, learning is inference because the parameters are treated as latent, random variables, so they can use normal variational inference or MCMC to compute a distribution over the parameters. Note that for 99% of deep learning practitioners, training is synonymous with learning as the practitioner will likely only be computing a single set of values (aka point estimate) for their weights.

Why is the ELBO difficult to optimize?

The task of bayesian inference is to compute the posterior p(z | x) of the model p(x, z) = p(x|z)p(z) where z is a latent variable. This is often intractable, so a bayesian may resort to approximating it with some easier distribution q(z) — this method is called variational inference . Usually the approximating distribution is chosen from a parameterized family of distributions. Thus q(z) is really the variational distribution q(z; lambda) for some chosen value lambda. How is this parameter lambda chosen?

A common method is to minimize the KL-divergence between the variational distribution and the true posterior, KL[q(z; lambda) || p(z | x)]. Of course, the posterior isn’t actually known, but if we break down this KL divergence, we see the following:

KL[q(z) || p(z | x)] = E_q(z)[log(q(z)) - log(p(z|x))]
= E_q(z)[log(q(z)) - log(p(x, z)/p(x))]
= E_q(z)[log(q(z)) - log(p(x, z)) + log(p(x))]
= E_q(z)[log(q(z)) - log(p(x, z))] + log(p(x))
= E_q(z)[log(q(z)) - log(p(x|z)) - log(p(z))] + log(p(x))

The KL divergence can be minimized up to a constant (the marginal likelihood) wrt the variational parameters since we know how to compute p(x, z) per the model’s definition. This term that we want to minimize — E_q(z)[log(q(z)) - log(p(x|z)) - log(p(z))] — is the negative evidence lower bound (ELBO). So, back to the original title question — why is the ELBO difficult (but not impossible) to optimize?

It actually isn’t difficult to optimize for certain classes of models. If all the latent variables are chosen to be independent in the variational distribution (i.e. the mean-field assumption) and the model is conditionally conjugate, then one can use coordinate ascent variational inference.  This method is fast to compute. Unfortunately, the restrictions it places on the model are also quite limiting. It is when the model is unconstrained is optimizing the ELBO difficult. But again, why?

If nothing is known about the model p(x|y)p(y) except a method to evaluate it, we are relegated to optimizing the ELBO by gradient descent. This entails computing the gradient of the ELBO (excuse my abuse of notation):

Gradient of E_q(z)[log(q(z)) - log(p(x|z)) - log(p(z))]
= gradient of (integral of q(z)*(log(q(z)) - log(p(x|z)) - log(p(z)))dz)
= gradient of (integral of q(z)*log(q(z))*dz) - (integral of q(z)*(log(p(x|z)) - log(p(z))*dz))
= integral of (gradient of q(z)*log(q(z))*dz)) - (integral of (gradient of q(z))*(log(p(x|z)) - log(p(z))*dz))

where the I've shortened q(z; lambda) to q(z) and the gradient is wrt lambda.

When I first saw this equation, I wasn’t sure what the big deal was. This is because I wasn’t accustom to staring at math equations all day, but to any (applied) mathematician it should be obvious. I’ll put in bold font: computing the gradient of the ELBO *requires computing some likely high-dimensional, likely intractable integral.* Why is it intractable? Well, you may get lucky and the integral has an analytic solution, but in general that won’t be true. Also, because  this quantity no longer takes the form of an expectation, it can’t easily be estimated by Monte Carlo. It may be possible to do so if z is discrete and its sample space is small (as you could exhaustively evaluate the integrand at all z), but that implies z is very low dimensional which may not be true either.

Luckily there exist some methods to side-step these issues by placing mild(ish)  constraints on either the variational family of distributions or both the variational family and the model. These methods are the score function gradient and reparameterization gradient, but I won’t be discussing them in this post — they’re best left to be explained another day (or by Google)..

Expectation Maximization vs Variational Bayes

I constantly find myself forgetting the details of the EM algorithm, variational bayes, and what exactly the difference is between the two. To avoid confusion in the future, I wrote the following note.

Q: What is the difference between EM and Variational Bayes (aka "Variational Bayesian EM")?
A: Both are iterative methods for learning about the parameters theta and the posterior p(z | x, theta) in a latent variable model p(x, z | theta) by trying to a maximize a lower bound to the marginal likelihood p(x) (or p(x | theta) when using EM). The difference between the two techniques lies in following:

1. VB assumes that, even when given a setting of the parameters theta, it is not tractable to compute the posterior p(z | x, theta). Thus, it must be approximated by some variational distribution q(z). On the other hand, EM makes the opposite assumption - given a setting of the parameters theta, it will compute the exact posterior p(z | x, theta). In this sense, VB is a relaxation of EM.
2. VB is a bayesian technique while EM is a frequentist technique. As such, VB treats theta as a latent, random variable and computes a distribution q(theta) that approximates the posterior distribution p(theta | x). EM, a maximum likelihood technique, computes a point estimate to the parameters theta instead of a full distribution.

With these differences in mind, we can describe the two algorithms using a similar framework.

Objective:
EM’s objective is to maximize a lower bound to p(x | theta),  E_q(z)[log(p(x, z | theta))].
VB’s objective is to maximize a lower bound to p(x), E_q(z, theta)[log(p(x, z, theta))].

E-step:
EM first maximizes the objective by fixing theta and then finding an optimal setting of q(z). This optimal setting is always calculated to be the posterior p(z | x, theta).
VM first maximizes the objective by fixing q(theta) and finding a better setting of q(z)  (often by some gradient method).

M-step:
EM maximizes the objective by fixing q(z) to the posterior from the previous E-step, and then calculates a maximum likelihood point estimate of the parameters theta.
VM maximizes the objective by fixing q(z) and then finding a better setting of q(theta) (again, often by some gradient method).

The E and M step are then repeated until convergence (i.e. until the point at which the log marginal likelihood no longer improves).

One last point: there is another algorithm called "Variational EM". This algorithm is just the E-step of VB combined with the M-step of EM. Since parameters are not treated as random variables, it is not a bayesian technique.

Frequentists vs Bayesians

A really wonderful aspect of learning about machine learning is that you can't help but learn about the field statistics as well. As a computer scientist (or really, a software engineer -- I have a hard time calling myself a computer scientist), one of the joys of the field is that many interesting problems require expertise from other fields and so computer scientists tend to be exposed to a great many of ideas (even if only in a shallow sense)!

One of the major divides among statisticians is in the philosophy of probability. On one hand there are frequentists who like to place probabilities only on data; there is some underlying process that the data describes, but one doesn't have knowledge of all data, so there only exists uncertainty about what unknown data the process could generate. On the other hand there are bayesians who, like the frequentists, place probabilities on data for the same reason, but who also place probabilities on the models they use to describe the underlying process and on the parameters of these models. They allow themselves to do this because they concede that, although there does exist one true model that could perfectly describe the underlying process, as the modeler they have their own uncertainty about what that model may be.

I think this is an interesting divide because it highlights two different sources of uncertainty. Some uncertainty exists because there exists true randomness in the world (or so physicists believe), while other uncertainty exists solely due to our own ignorance -- the quantity in question may be completely determined! We are just forced to work with incomplete information. I think it is fascinating that there exists a unified framework that allows us to manage both sources of uncertainty, but it does make me wonder: do these two sources of uncertainty warrant their own frameworks?

An intuition of Newton's method

During my lazy weekend afternoons (and all the other days of the week) I've been going through Nando de Freitas' undergraduate machine learning course on youtube. In lecture 26 he introduces gradient descent, an iterative algorithm for optimizing (potentially non-convex) functions. I'll refrain from explaining gradient descent more than that as there are many good explanations on the internet (including Professor de Freitas'), but I do want to discuss gradient descent's learning rate parameter and why intuitively Newton's method, also introduced in lecture 26, is able to side-step the learning rate.

As described in the video lecture, a common difficulty with gradient descent is picking the learning rate hyper-parameter. Pick too small of a learning rate and gradient descent will come to crawl and make very little progress or even eventually stop making progress due to floating point underflow. Pick too large of a learning rate and gradient descent will oscillate around the minimum/maximum, bouncing around, very slowly making progress. In an ideal world, as the gradient vanishes, the gradient descent algorithm would be able to compensate by adjusting the learning rate so to avoid both underflow and oscillation. This is exactly what Newton's method does.

Compare gradient descent
$$\boldsymbol\theta _{k+1} = \boldsymbol\theta _{k} - \eta_{k}\nabla f(\boldsymbol\theta_{k})$$
to Newton's method
$$\boldsymbol\theta _{k+1} = \boldsymbol\theta _{k} - H_{k}^{-1}\nabla f(\boldsymbol\theta_{k})$$

The only difference is that Newton's method has replaced the learning rate with the inverse of the Hessian matrix. The lecture derived Newton's method by showing that \(f(\boldsymbol\theta)\) can be approximated by a second-order Taylor series expansion around \(\boldsymbol\theta_{k}\). If you're familiar with Taylor series, then this explanation may be sufficient, but I prefer to think about it differently.

What is this Hessian matrix we've replace the learning rate with? Just as the gradient vector is the multi-dimensional equivalent of the derivative, the Hessian matrix is the multi-dimensional equivalent of the second-derivative. If \(\boldsymbol\theta_{k}\) is our position on the surface of the function we're optimizing at time step \(k\), then the gradient vector, \(\nabla f(\boldsymbol\theta_{k})\), is our velocity at which we're descending towards the optimum, and the Hessian matrix, \(H\), is our acceleration.

Let's think back to the original problem of choosing the learning rate hyper-parameter. It is often too small, causing underflow, or it is too big, causing oscillation, and in an ideal world we could pick just the right the learning rate at any time step, most likely in relation to the rate at which the gradient vector vanishes, to avoid both these problems. But wait, now we have this thing called the Hessian matrix that measures the rate at which the gradient vanishes!

When starting the algorithm's descent we will quickly gain acceleration as we starting going downhill along the function's surface (i.e. the Hessian matrix will "increase"). We don't want to gain too much velocity else we'll overshoot the minimum and start oscillating, so we'd want to choose a smaller learning rate. As the algorithm nears the optimum, the geometry of the function will flatten out and we will eventually lose acceleration. We don't want to lose too much velocity else we'll underflow and stop making progress. It is precisely when we lose acceleration (i.e. the Hessian matrix "decreases") that we want to increase our learning parameter.

So we have observed that heir is an inverse relationship between the magnitude of the acceleration at which we descend towards the minimum and the magnitude of the most desirable learning parameter. That is to say, at greater accelerations we want smaller learning rates and at smaller accelerations we want larger learning rates. It is precisely for this reason why Newton's method multiplies the gradient vector (the "velocity") by the inverse Hessian matrix ("the inverse acceleration")! At least, this is how I intuitively think about Newton's method. The derivation involving Taylor series expansions is probably the actual precise reason, but I like thinking about it in terms of velocities and accelerations.

Finally, I'd like to end with one cautionary note. I'm an amateur mathematician. I like to think my intuition is correct, but it may not be. By sharing my intuition, I hope to help others who are looking to gain intuition, but if you need anything more than an intuitional understanding of Newton's method or gradient descent (because perhaps you're an actual mathematician in training), please consult a textbook or your favourite professor :-).

On optimizing high-dimensional non-convex functions

Excuse me for the (in)completeness of this post. What follows is merely a thought, inspired by two independent statements, about a domain of science (or math, really) with which I am barely initiated. Let me give you these two statements first.

In the book Foundations of Data Science, the very first paragraph of the book says

If one generates n points at random in the unit d-dimensional ball, for sufficiently large d, with high probability the distances between all pairs of points will be essentially the same. Also the volume of the unit ball in d-dimensions goes to zero as the dimension goes to infinity. 

That is statement one. Statement two is an assertion given in this year's Deep Learning Tutorial at the Neural Information Processing Systems (NIPS) conference. They claim that "most local minima are close to the bottom (global minimum error)."

The second statement is significant for training (deep) neural networks. Training a neural network always uses a variant of a gradient descent, a method for minimizing the neural network's error by iteratively solving for when the gradient (i.e. the derivative) of the function that gives the error is 0. Ideally gradient descent will approach the global minimum error (the point where the neural network will give the most desirable approximations of the training data), but that is only guaranteed when the error function is convex (there are no hills when the function is plotted). Unfortunately, a neural network almost never has a convex error function. Hence, during gradient descent, one might find a local minimum that is nowhere near as low as the global minimum. The second statement however says we shouldn't be so concerned -- all local minima will be close to the global minimum!

But why?

My thought is that somehow the first statement can be used to prove the second statement. The training data of modern neural networks is high dimensional. It will also often be normalized as part of feature scaling. Given those two properties, the high-dimensional hills and valleys of a neural network's error function then (roughly) form unit hemispheres. This (possibly) implies that that local minima are close to the global minimum because the volumes of every valley nears zero, making all the valleys increasing similar to each other as the dimensionality of the training data increases.

I want to stress though, this is a half-baked idea. It's probably rubbish. It might also be redundant! Perhaps the second statement already has a proof and I've missed it. Either way, I would love to see if others find my intuition plausible or, even better, to be pointed in the direction of a proof for the second statement.

TIL: premultiplied-alpha colors

Alpha is the measure of how translucent an object is. An alpha of 0.0 means the object is entirely transparent, an alpha of 1.0 means the object is entirely opaque, and an alpha in the middle means a fraction of the total light may passthrough the object. Traditionally, a color is represented by 4 constituent components: a red contribution, a green contribution, a blue contribution, and the alpha. When compositing two colors together, one on top of the other, the alpha acts as a modulus of the colors, indicating how much of the top color and how much of the bottom color contribute to the new composited color. The traditional compositing operation is as follows, where A is being composited over top B:


Alternatively, we may wish to premultiply the red, green, and blue components by the alpha:


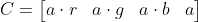
With this representation we get a new compositing equation:

This new form is interesting for a couple reasons.

1. It is computationally more efficient. It requires one less vector multiplication.
2. It is a closed form. Compositing a premultiplied-alpha color over top a premultiplied-alpha color yields another premultiplied-alpha color. The same cannot be said of non-premultiplied-alpha colors. Compositing two non-premultiplied-alpha colors yields, interestingly, a premultiplied-alpha color.
3. When filtering (aka downsampling), it produces more visually accurate results. A picture is worth a thousands words.

And that's it. Premutliplied-alpha colors are nifty.