Regarding my last post, I'm glad to see I'm in good company in feeling that object-oriented programming is not the be-all, end-all to software design (nor is it always a good design). Now if only I could get my school's Software Engineering department to agree...
I should also note, I have a lot more to my opinion than what I crudely wrote in my last post. I just don't feel particularly motivated to expand upon them because religion is religion is religion and I doubt anyone reading this (if there is anyone reading this) will alter their views based on what I have to say.
Wednesday, November 14, 2012
Thursday, October 18, 2012
On the Harm of Object-Oriented Programming
This is an excerpt of an essay that I wrote for a class, prompted by Dijkstra's famous goto letter. I must admit that it was written in a very "stream-of-conscious" type of way, so it may not be elegant writing, but I think it's worth putting down anyways.
I believe today that the reach of computer science (which I should probably refer to as software engineering as the discussions of goto is more a practical than a theoretical) is sufficiently widespread that is has divided the industries of programming so much that it is not useful or plausible to talk of a single language feature or programming practice being useful or harmful. What is useful for a web application could be considered harmful for an embedded software application, and vice-versa. So I would limit my response to the area that I most familiar: desktop application development.
In my opinion, one of the most harmful programming features is single-paradigm object-oriented programming. Object-oriented programming has been advocated, pushed, and taught so strongly for the past 20 years that it is almost universally used to model any problem we need to tackle as programmers. However, like any tool, there are strengths and weaknesses. At the heart of object-oriented programming, the idea is to model every piece of the program as realistically as possible to a noun that as humans we can understand (which implies that we are attempting to draw a parallel between real life objects and our programs). The consequence is that we group pieces of data that compose that noun together in memory. This has significant downsides on modern desktop computers though. This grouping of data that object-oriented programming encourages is essentially the memory layout referred to as “array of structures” (AOS). Consider an AOS layout for a list of particles being used to model an explosion effect in a video game. In this setup, you may have a geometric vector for a position, velocity, force stored in this object. Presumably, since the particle has these attributes, you need to perform a numerical integration of these attributes over time. This is a loop over your particles where at each iteration you access each attribute, perform the necessary computation, and store the result. In the AOS layout, these properties are stored contiguously in memory and further each particle is stored contiguously in memory. That means on current desktop PCs, where memory access is expensive and the hardware has a lot of builtin mechanisms to reduce the costs, the particle array will only utilize one cache line. On the contrary, let’s reconsider the system we’re building. We designed our program so that each particle is an object. But when will there only exist one particle? The answer is never. The program can be better redesigned to account for the fact that particles are only ever used in mass. So the solution is to split each attribute of a particle into an array of each attribute (the so called “structure of array” layout), and now when iterating over the particle data there will be a cache line utilized by each array, significantly reducing the amount of cache miss and increasing the performance of the application. Arguably you can still have a “ParticleManager” object, so all hope isn’t lost for object-oriented programming; but the point is that single paradigm object-oriented programming languages are so taught and widely used that the mindset we’ve learned has lead us to design our particle system blindly, thinking about real-world abstraction instead of an abstraction that makes sense for both us and the computer. On a final note, I talk of single paradigm object-oriented programming because it is those languages that force us to think in terms of object and don’t allow us to escape the paradigm when it no longer makes sense.
Sunday, May 27, 2012
Animating NSSplitView
A couple of days ago I set out to come up with an emulation of Mail.app's "Mail Activity" panel. For the most part, it was a straight forward implementation. Create a horizontal NSSplitView in IB, set the top view to my source list (or whatever else you want -- it doesn't matter), set the bottom view to a custom view whose drawRect: method have been overridden to draw a background color matching the source list background color.
Okay, that's fine and dandy. All that's left is to implement the "Show/Hide" toggle functionality. There were two constraints I wanted to make sure I abided by:
This can be added as either a category extension or in a subclass. To actually restore the panel to it's previous height is dead simple once you have this. Upon hiding you call positionForDividerAtIndex: on the panel's parent split-view and save the value, and then upon unhiding you use the saved value to set the divider's new position.
Okay, so that does it for my explanation of Core Animation. Know the kicker: how so animate something that isn't associated with a property (such as setPosition:ofDividerAtIndex:)? My solution? Create a faux key path! By overriding animationForKey:, valueForUndefinedKey: and setValue:forUndefinedKey: and creating setPosition:ofDividerAtIndex:animate: to initiate the animation, I can trick the view into thinking properties exist for each divider. The faux key path is a series of key paths, one for each divider (which I call "dividerPosition0", "dividerPosition1", "dividerPosition2", etc..) and a catch-all key "dividerPosition" that all dividers can use if the user doesn't provide an animation specific to that divider.
setPosition:ofDividerAtIndex:animate: is straightforward. It calls the original setPosition:ofDividerAtIndex: if animate is false, else it calls setValue:forKey on the animator proxy with the appropriate dividerPosition key.
The other three methods are small also, but share in common the need to parse the key to check whether the key is a valid "dividerPositionN" key, and if so extract that 'N' suffix integer value for use. animationForKey: will first check whether an animation all ready exists for the key, and if an animation doesn't it will return the defaultAnimation for the "dividerPosition" key.
And finally, valueForUndefinedKey: and setValue:forUndefinedKey: are just wrappers around positionForDividerAtIndex: and setPosition:ofDividerAtIndex:
And that's it! I stick this code in a NSSplitView subclass, and animate a divider by calling [mySplit setPosition:pos ofDividerAtIndex:divIndex animate:YES].
I hope you've enjoyed this post and find the code useful. However, this code is young and not well-tested. If you come across any problems or have suggestions I'd love to hear them in the comments section. Until next time.. :)
Okay, that's fine and dandy. All that's left is to implement the "Show/Hide" toggle functionality. There were two constraints I wanted to make sure I abided by:
- When toggling from hidden to shown, I want to restore the panel's height to it's previous height when it was last shown.
- I want the toggle to animate like in Mail.
Restoring the previous height
I can't fathom why, but NSSplitView has a method to set a divider's position (setPosition:ofDividerAtIndex:), but doesn't have a method to query a divider's position. The implementation is trivial, but that just makes me wonder all the more why NSSplitView doesn't have it. Maybe I'm overlooking something, and my implementation is horribly broken; I'm not really sure! But let's assume and hope that I'm not too far off :). Here's my implementation:- (CGFloat)positionForDividerAtIndex:(NSInteger)idx
{
NSRect frame = [[[self subviews] objectAtIndex:idx] frame];
if (self.isVertical) {
return NSMaxX(frame) + ([self dividerThickness] * idx);
}
else {
return NSMaxY(frame) + ([self dividerThickness] * idx);
}
}
This can be added as either a category extension or in a subclass. To actually restore the panel to it's previous height is dead simple once you have this. Upon hiding you call positionForDividerAtIndex: on the panel's parent split-view and save the value, and then upon unhiding you use the saved value to set the divider's new position.
Animating the panel
My initial reaction was to animate the frame of the panel view using NSView's animator proxy object. However, that just felt messy to me. There were to many unknowns in my mind -- how would changing the frame of subview interact with the rest of NSSplitView? My guess it that I'd most likely need to animate all subviews of the NSSplitView and do some additional magic in the NSSplitView's delegate methods. I quickly dismissed this option.
My second thought was to somehow animate the split view's divider itself (which you might of guessed by the previous section on restoring a divider's position). This should correctly size the subviews and obey any constraints imposed by the NSSplitView's delegate. The problem is that Core Animation relies on key-value coding to animate arbitrary properties of a class. And although conceptually each divider's position kinda-sorta feels like a property, they aren't. But that was my inspiration!
Before I get into the implementation, let me briefly describe how Core Animation can animate arbitrary properties. The first requirement for the class whose properties you want to animate is for the class to implement the NSAnimatablePropertyContainer protocol. To my knowledge, NSView and NSWindow are the only classes in AppKit that implement this protocol, and there isn't a way to implement this yourself without Apple's SPI. Part of NSAnimatablePropertyContainer is the animator method. It returns a proxy object responsible for initiating animations (the proxy object can also be treated and passed around just like the original object because it will respond to any method the original object responds to). The magic works by checking whether messages sent to the animator proxy conform to a property's key path on the original object. If it does, it will check with its animationForKey: to see if there exists an animation associated with that property, and there does then it will do magic, private CoreAnimation operations to perform the animation using a series of setValue:forKey: method calls for each sample along the animation. If the sent message either doesn't have an associated animation or doesn't represent a proper key-value compliant property, then the proxy will just forward the method to the original object.
So, to animate custom properties that don't have default animations (such as frame or position do) we have to create and associate an animation of our choosing with the property, and then send the appropriate method to the animator proxy object. Here's a quick example to check out.
@interface MyCustomView : NSView
@property (assign) float customAnimatableProperty;
@end
@implementation MyCustomView
@synthesize customAnimatableProperty;
- (void)testAnimation
{
// Add a custom animation to the animations dictionary
CABasicAnimation* animation = [CABasicAnimation animation];
NSMutableDictionary* newAnimations = [NSMutableDictionary dictionary];
[newAnimations addEntriesFromDictionary:[self animations]];
[newAnimations setObject:animations forKey:@"customAnimatableProperty"];
[self setAnimations:newAnimations];
// initiate the animation
[[self animator] setCustomAnimatableProperty:10.0f];
}
@end
Okay, so that does it for my explanation of Core Animation. Know the kicker: how so animate something that isn't associated with a property (such as setPosition:ofDividerAtIndex:)? My solution? Create a faux key path! By overriding animationForKey:, valueForUndefinedKey: and setValue:forUndefinedKey: and creating setPosition:ofDividerAtIndex:animate: to initiate the animation, I can trick the view into thinking properties exist for each divider. The faux key path is a series of key paths, one for each divider (which I call "dividerPosition0", "dividerPosition1", "dividerPosition2", etc..) and a catch-all key "dividerPosition" that all dividers can use if the user doesn't provide an animation specific to that divider.
setPosition:ofDividerAtIndex:animate: is straightforward. It calls the original setPosition:ofDividerAtIndex: if animate is false, else it calls setValue:forKey on the animator proxy with the appropriate dividerPosition key.
- (void)setPosition:(CGFloat)position ofDividerAtIndex:(NSInteger)dividerIndex animate:(BOOL)animate
{
if (!animate) {
[super setPosition:position ofDividerAtIndex:dividerIndex];
}
else {
[[self animator] setValue:[NSNumber numberWithFloat:position] forKey:[NSString stringWithFormat:@"dividerPosition%i", dividerIndex, nil]];
}
}
The other three methods are small also, but share in common the need to parse the key to check whether the key is a valid "dividerPositionN" key, and if so extract that 'N' suffix integer value for use. animationForKey: will first check whether an animation all ready exists for the key, and if an animation doesn't it will return the defaultAnimation for the "dividerPosition" key.
- (id)animationForKey:(NSString *)key
{
id animation = [super animationForKey:key];
NSInteger idx;
if (animation == nil && [self _tryParsingDividerPositionIndex:&idx fromKey:key]) {
animation = [super animationForKey:@"dividerPosition"];
}
return animation;
}
And finally, valueForUndefinedKey: and setValue:forUndefinedKey: are just wrappers around positionForDividerAtIndex: and setPosition:ofDividerAtIndex:
- (id)valueForUndefinedKey:(NSString *)key
{
NSInteger idx;
if ([self _tryParsingDividerPositionIndex:&idx fromKey:key]) {
CGFloat position = [self positionForDividerAtIndex:idx];
return [NSNumber numberWithFloat:position];
}
return nil;
}
- (void)setValue:(id)value forUndefinedKey:(NSString *)key
{
NSInteger idx;
if ([value isKindOfClass:[NSNumber class]] && [self _tryParsingDividerPositionIndex:&idx fromKey:key]) {
[super setPosition:[value floatValue] ofDividerAtIndex:idx];
}
}
And that's it! I stick this code in a NSSplitView subclass, and animate a divider by calling [mySplit setPosition:pos ofDividerAtIndex:divIndex animate:YES].
I hope you've enjoyed this post and find the code useful. However, this code is young and not well-tested. If you come across any problems or have suggestions I'd love to hear them in the comments section. Until next time.. :)
Wednesday, March 21, 2012
Never do this:
Rename libc++.1.dylib (in /usr/lib) to something other than libc++.1.dylib. I wanted to install a fresh svn build of libc++ on my home computer. I figured I wanted to keep the original dylib file around just incase anything went horribly wrong (TM). The irony? Renaming libc++.1.dylib basically made my whole machine fail. Internet stopped working, Finder stopped working, spotlight stopped working, launchd crashed on reboot causing my computer to hang, and who know what else was broken because of it.
In hindsight, I guess it makes sense that renaming libc++.1.dylib would cause a lot of stuff to crash since libc++ is a dynamically loaded library. Though I always thought that when a dylib was loaded, it was somehow copied into the resident memory of the application. I guess not.
It does make me wonder though... what IS the correct way to install libc++ if not to replace the file? libc++'s website suggests creating links in /usr/lib but goes on to say "either way to should work" (and then never goes on to say what that other way is..). Hum.
And just to document what I did to fix it:
In hindsight, I guess it makes sense that renaming libc++.1.dylib would cause a lot of stuff to crash since libc++ is a dynamically loaded library. Though I always thought that when a dylib was loaded, it was somehow copied into the resident memory of the application. I guess not.
It does make me wonder though... what IS the correct way to install libc++ if not to replace the file? libc++'s website suggests creating links in /usr/lib but goes on to say "either way to should work" (and then never goes on to say what that other way is..). Hum.
And just to document what I did to fix it:
- Booted into single user mode (held command-s during reboot).
- Saw a diagnostic message saying that stuff crashed because libc++.1.dylib was missing. This is when I realized that renaming libc++.1.dylib did have such catastrophic effects.
- Rebooted into recovery mode (held command-r during reboot).
- cd up several directories until I found "Volumes"
- cd into Volumes/Macintosh\ HD/usr/lib
- renamed the file to libc++.1.dylib (using the 'mv' command).
- Rebooted normally, and prayed that this would fix it
- And it did!
Sunday, March 11, 2012
Matrix-Vector Multiplication
I'm finishing up my spring break this week (I know - not much of a "spring" break, but you take what you can get) and I decided to start going through the MIT OpenCourseWare course on Linear Algebra. I want to be a graphics guy when I get out of school and I haven't taken a single linear algebra course yet! Shame on me.
Gilbert Strang is a great lecturer. He teaches linear algebra in a such a way that even the small points he makes makes you go "aha!" I'd never had matrix-vector multiplication explained to me; it was just something I memorized and had to take a leap of faith for. In his lectures, Strang really hits home the importance of this idea of "linear combinations."
Linear combinations are simple. If you have a bunch of vectors and a scalar coefficient for each vector, the linear combination is just the addition of each vector multiplied by its scalar.
As it turns out, that's exactly what matrix-vector multiplication is, too. Each column in your matrix is one of the vectors and each component in your vector is one of the coefficients (the first component of the vector is the coefficient to the first column, the second component of the vector is the coefficient to the second column, etc.).
The typical way to think of matrix-vector multiplication is to just consider your vector as a matrix and do the standard "take a row from the first matrix, take a column from the second matrix, perform the dot product" matrix multiplication.
With the linear combination concept, matrix-vector multiplication becomes much more intuitive (for me at least) because it's just a normal linear combination:
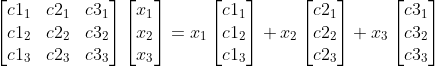
The linear combination repurposing of matrix-vector multiplication makes a lot of sense if you imagine the matrix to be a rotation matrix where each column is an axis that forms a basis/coordinate system, and the vector to be a point in space. If you visualize vector addition using the "head-to-tail" concept, you can almost visualize why multiplication of a rotation matrix and a point works!
Gilbert Strang is a great lecturer. He teaches linear algebra in a such a way that even the small points he makes makes you go "aha!" I'd never had matrix-vector multiplication explained to me; it was just something I memorized and had to take a leap of faith for. In his lectures, Strang really hits home the importance of this idea of "linear combinations."
Linear combinations are simple. If you have a bunch of vectors and a scalar coefficient for each vector, the linear combination is just the addition of each vector multiplied by its scalar.
As it turns out, that's exactly what matrix-vector multiplication is, too. Each column in your matrix is one of the vectors and each component in your vector is one of the coefficients (the first component of the vector is the coefficient to the first column, the second component of the vector is the coefficient to the second column, etc.).
The typical way to think of matrix-vector multiplication is to just consider your vector as a matrix and do the standard "take a row from the first matrix, take a column from the second matrix, perform the dot product" matrix multiplication.
With the linear combination concept, matrix-vector multiplication becomes much more intuitive (for me at least) because it's just a normal linear combination:
The linear combination repurposing of matrix-vector multiplication makes a lot of sense if you imagine the matrix to be a rotation matrix where each column is an axis that forms a basis/coordinate system, and the vector to be a point in space. If you visualize vector addition using the "head-to-tail" concept, you can almost visualize why multiplication of a rotation matrix and a point works!
Friday, March 2, 2012
Computability and the Underpinnings of Computer Science
This week I concluded a course I took this quarter that covered the theory behind computer science. How comprehensive the course's coverage of a whole field's underpinnings was, I'm not qualified to speculate (but my guess would be: not very). With that said, it did cover a lot of interesting material. The course covered:
- The Chomsky hierarchy of formal languages.
- Regular languages/(non-deterministic and deterministic) finite state automata/regular expressions/left-linear and right-linear context-free grammars.
- Pumping lemma for proving non-regularity of languages
- Deterministic push-down automata (and whatever class of languages these are equivalent to)
- Context-free grammars/push-down automata
- Ambiguity
- Griebach Normal Form
- Chomsky Normal Form and membership test Cocke-Younger-Kasami (CYK) algorithm.
- Pumping lemma for proving language to be not context-free.
- An offhand mention of context-sensitive language
- Recursively enumerable languages/Turing Machines.
- Computability (unfortunately we were not able to solve does P=NP and win that new car).
- P time
- NP time
- NP-hard vs. NP-complete vs. NP
- Decidability vs. intractability
What I was disappointed about was the treatment of computability and exactly what the heck it means to be P or NP. I came away feeling only a little less confused about the problem than I was when I started the class.
As always, I went to google. I found a great explanation on stackoverflow (scroll to grom's answer) that was a good balance between layman's terms and formal terms I learned in class.
From my understanding now:
- P problems are a class of problems where there is a known algorithm that can provide an answer/solution to the problem in polynomial time. Polynomial time can be O(1), O(n), or O(n^100000000). It doesn't matter.
- NP problems are a class of problems where we can guarantee there exists a solution, but we can't compute it in polynomial time; it can only be computed in non-deterministic polynomial time. What that means is that there exists a finite, polynomial amount of steps to find the solution but we can't describe a polynomial algorithm to reach it. We have to resort to an exhaustive, "brute-force" search for the solution. This is a problem because some NP problems are intractable which means even though it's possible to find an answer it may take so long it's not even worth it.
- NP-complete problems are problems that are NP but have the special property that all other NP problems can be reduced to them in polynomial time. This "simply" means any NP problem can be transformed into the NP-complete problem using a polynomial time algorithm.
- NP-hard problems are problems that are at least as difficult to solve as the hardest NP problem(s). Note, this class of problems includes problems that are harder than any NP problem (which means they may not even be solvable in non-deterministic polynomial time).
Subscribe to:
Posts (Atom)